题目

Problem Description

RC非常喜欢一个名叫"Lie Dice"的游戏，并立志要成为当中的牛人。后来他听说有一位成为"骰神"的世外高手，就来到了骰神的住所，想拜骰神为师。开始时骰神将他拒绝了，但在RC的死缠烂打之下，骰神终于心软，不过提出要经过一场入门考验。
骰神的考验是这样的：在骰神的园子里有一个N*M的矩形地，里面是N行M列的小方格。对每一行按从南到北的顺序由1-N编号，对每一列按从西到东的顺序由1-M编号，每个小方格用它的行列编号来表示，即(i,j)表示第i行第j列的方格。这样最西南的方格就是(1,1)，最东北的方格就是(n,m)。
骰神在(1,1)的方格中放置了一颗骰子，其中点数1向上。骰子可以往东南西北四个方向滚动，滚动之后骰子就到了该方向的下一格，但同时点数1的朝向也可能会发生变化。如最开始将骰子往北滚动，骰子就到了(2,1)处，此时点数1向北。
可怜的RC想了很久，还是没有想出办法。他郁闷地往回走时，突然碰到一个乞丐。乞丐望了他两眼，惊异地说："不得了了，不得了了。你有一道灵光从天灵盖中喷出，年纪轻轻就有一身投机的气质，真是百年难得一见的赌博奇才。若让你打开任督二脉，你还不会飞骰啊？今天看你我有缘，我这里有一本秘笈，就便宜点10块钱卖给你吧！"
RC定睛一看，这是一本名为《骰神秘笈》的方格簿。RC翻开第一页，上面赫然写着："你还在为通不过滚骰考验而困扰吗？来吧，只要拨打以下热线号码，包你轻松过关！"
RC拨完那个号码后，你的电话突然响起，原来那是你的号码。那么，你能帮帮他吗？

Input

输入有多组数据。每组数据仅有一行，当中有两个正整数X和Y，表示要将骰子滚到(X,Y)处，且点数1向上。X=Y=0时表示输入结束。
1<=X,Y<=100000000

Output

对于每组数据输出一行，仅包含一个整数，即最少要滚动的次数。

Sample Input

1 1
1 2
1 5
0 0

Sample Output

0
3
4

解题思路

注意：

1. 为了便于描述，接下来的描述将 “1” 的朝向称为骰子的朝向。
2. 为了便于取模后的计算，行列的编号改成从 0 开始。

首先要知道几个规律：

• 骰子往同一方向连续滚动 4 次，骰子的朝向跟滚动之前相同。
• 骰子往东或西连续滚动 2 步，再往南或北连续滚动 2 步，骰子的朝向跟滚动之前相同。
• 骰子往南或北连续滚动 2 步，再往东或西连续滚动 2 步，骰子的朝向跟滚动之前相同。
• 骰子处于东西朝向时，骰子往南北滚动，不影响骰子的朝向。
• 骰子处于南北朝向时，骰子往东西滚动，不影响骰子的朝向。

另外

• 骰子处于东西朝向时，如果想令骰子在相邻格子上处于南北朝向，则需要借助额外的两个方格。

现在开始分析题目：

由于行列的编号改成从 0 开始，所以骰子从 (0, 0) 开始滚动。

• 当 X = 0 时（即骰子不需要横向滚动时），分两种情况考虑：

  • Y 是 4 的倍数，这时骰子只需要直接往北滚动 Y 次到 (0, Y)，总步数 Y;

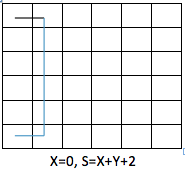
  • 如果 Y 不是 4 的倍数，则先往东滚动一步至 (1, 0)，使骰子朝东，再往北滚动 Y 次到 (1, Y)，再往西滚动一步即可。总步数 Y + 2（如下图所示）；

    

• 当 X = 1 时，分三种情况考虑：

  • Y = 1，此时至少需要 6 步；

  • Y 是 4 的倍数，这时骰子先往北滚动一步，令骰子朝北，再往东滚动 X 步（即 1 步），到达 (X, 1)，再连续往北滚动到 (X, Y)，总步数 X + Y（如下图所示）；

    

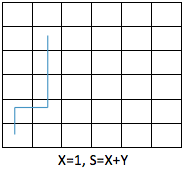
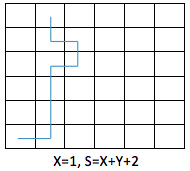
  • Y 不是 4 的倍数，这是骰子先往东滚动一步，令骰子朝东，再连续往北滚动至 (1, Y - 2)，这时来一个“辅助转向”，使得骰子在 (1, Y - 1) 朝南，再往北滚动一步，到达 (X, Y)，总步数 X + Y + 2（如下图所示）；

    

• 当 X > 1 时，按 X % 4 的结果分四种情况考虑：

  先考虑结果为 2 和 3 的情况：

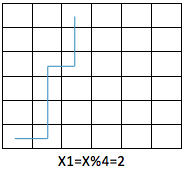
  • 结果为 2，则骰子先往东滚动 (X % 4 * 4) 步至 (X - 2, 0)，再往东滚动一步至 (X - 1, 0)，这时骰子朝东，再往北滚动至 (X - 1, Y - 2)，再往东滚动一步至 (X, Y - 2)，这时骰子朝下，再往北连续滚动两次即到达 (X, Y)。总步数 X + Y（如下图所示）；

    

  • 结果为 3，则骰子先往东滚动 (X % 4 * 4) 步至 (X - 3, 0)，然后往北滚动一步至 (X - 3, 1)。这时骰子朝北来一个“特殊的”辅助转向，先往东滚动一步，再往北，再往东，使得骰子朝西（特殊之处在于骰子在最后一步返回相邻方格的时候往相反方向滚动了）。接下来向北连续滚动至 (X - 1, Y)，再往东滚动一步即到达 (X, Y)。总步数 X + Y（如下图所示）；

    

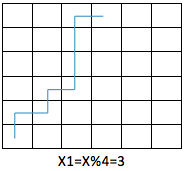
  现在来考虑剩下的结果为 0 和 1 的情况：

  • 结果为 0，可以先运用规律（往东连续滚动两步，再连续往北滚动两步）使得骰子来到 (2, 2)且朝上，这时剩下的路程按照上面结果为 2 的方法走完即可；
  • 结果为 1，可以先运用规律（往东连续滚动两步，再连续往北滚动两步）使得骰子来到 (2, 2)且朝上，这时剩下的路程按照上面结果为 3 的方法走完即可。

从上面的分析可以看出，最少滚动次数的实现方法可以总结为：将几个规律组合起来使用，并以尽量少走回头路和少走额外方格的方式将 X 跟 Y 的路程走完。

解题代码

//
//  main.cpp
//  骰神秘笈
//
//  Created by Yeah on 14-7-16.
//  Copyright (c) 2014年 Yeah. All rights reserved.
//

#include <iostream>

using namespace std;

void swap(int &a, int &b)
{
    int temp(a);
    a = b;
    b = temp;
}

int main()
{
    int X(0), Y(0);
    while (cin >> X >> Y && (X||Y))
    {
        if (X > Y)
        {
            swap(X, Y);
        }
        
        X--; //转换成坐标从 0 开始的坐标系坐标
        Y--;
        
        if (X == 0)
        {
            if (Y % 4 == 0)
            {
                cout << Y << endl;
            }
            else
            {
                cout << Y + 2 << endl;
            }
        }
        else if (X == 1)
        {
            if (Y == 1)
            {
                cout << 6 << endl;
            }
            else if (Y % 4 == 0)
            {
                cout << X + Y << endl;
            }
            else
            {
                cout << X + Y + 2 << endl;
            }
        }
        else
        {
            cout << X + Y << endl;
        }
    }
    return 0;
}

题目链接：无