题目
Problem Description
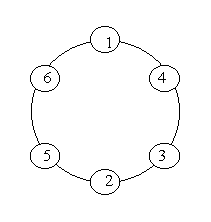
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6
8
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
解题思路
深度优先搜索,最难的也就是判断头尾两个相加起来是否为质数
代码速度跟内存占用都很糟糕的样子,就看看思路吧,欢迎吐槽_(:зゝ∠)_
解题代码
//
// main.cpp
// Prime Ring Problem
//
// Created by Yeah on 14-5-19.
// Copyright (c) 2014年 Yeah. All rights reserved.
//
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
bool isPrime(unsigned int n)
{
for (unsigned int i(2); i * i <= n; i++)
{
if (n % i == 0)
return false;
}
return true;
}
void stack_output(stack<unsigned int> s)
{
vector<unsigned int> reverse;
while(!s.empty())
{
reverse.push_back(s.top());
s.pop();
}
if (!isPrime(*reverse.begin() + *reverse.rbegin()))
{
return;
}
bool first_output(true);
for (vector<unsigned int>::reverse_iterator rit(reverse.rbegin()); rit != reverse.rend(); ++rit)
{
if (first_output)
{
cout << *rit;
first_output = false;
}
else
{
cout << ' ' << *rit;
}
}
cout << endl;
}
void DFS(vector<pair<unsigned int, bool> > &v,
stack<unsigned int> &s,
const unsigned int &n)
{
if (s.size() == n)
{
stack_output(s);
return;
}
for (vector<pair<unsigned int, bool> >::size_type pos(1); pos != v.size(); pos++)
{
if (s.size() == 0)
{
(v.begin() + pos)->second = true;
s.push((v.begin() + pos)->first);
DFS(v, s, n);
s.pop();
(v.begin() + pos)->second = false;
}
else if (!(v.begin() + pos)->second && isPrime((v.begin() + pos)->first + s.top()))
{
(v.begin() + pos)->second = true;
s.push((v.begin() + pos)->first);
DFS(v, s, n);
s.pop();
(v.begin() + pos)->second = false;
}
else
{
continue;
}
}
return;
}
int main(int argc, const char * argv[])
{
unsigned int n(0);
unsigned int Case_cnt(0);
while (cin >> n)
{
cout << "Case " << ++Case_cnt << ":" << endl;
vector<pair<unsigned int, bool> > v(n, pair<unsigned int, bool>(0, false));
stack<unsigned int> s;
for (vector<pair<unsigned int, bool> >::iterator it(v.begin()); it != v.end(); it++)
{
it->first = it - v.begin() + 1;
}
s.push(v.begin()->first);
DFS(v, s, n);
cout << endl;
}
return 0;
}